
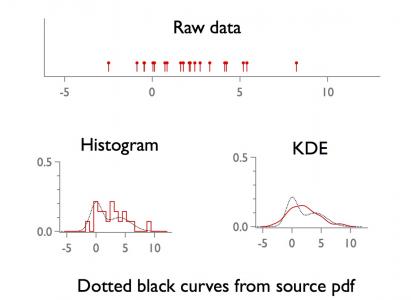
kernel density estimation (1d)

bech
Wed, 05/15/2013 - 12:47 pm
FastGaussTransform can be used to create a wrapper routine. The routine below is a minimal implementation. The attached experiment shows how to use it on simulated data.Caution:
FastGaussTransform saves time for large n by clustering nearby points. The cluster algorithm needs parameters (e.g., the /RX flag...) and the value chosen here probably does not always work. One symptom of "failure" is a jump discontinuity in the resulting pdf estimate. (It should be smooth.)kde is particularly nice for 2d (bivariate) data. One advantage is that you can generate smooth contours from the estimated pdf.
FastGaussTransform can handle such data, but it is not implemented below.Function kde(w,bw) // 1d kernel density estimation (Gaussian kernel)
wave w; variable bw // w must not contain NaNs
variable n=numpnts(w),kde_norm, xmin=wavemin(w)-2*bw, xmax=wavemax(w)+2*bw
variable nx = min(round(100*(xmax-xmin)/bw),100)
make /d/free/n=(n) wweights=1
FastGaussTransform /WDTH=(bw)/RX=(4*bw) /OUT1={xmin,nx,xmax} w,wweights // you may need to tweak /RX flag value
wave M_FGT; kde_norm=sum(M_FGT)*deltax(M_FGT); M_FGT /= kde_norm
string wn=NameofWave(w)+"_kde"; duplicate /d/o M_FGT $wn
killwaves M_FGT
End
wave w; variable bw // w must not contain NaNs
variable n=numpnts(w),kde_norm, xmin=wavemin(w)-2*bw, xmax=wavemax(w)+2*bw
variable nx = min(round(100*(xmax-xmin)/bw),100)
make /d/free/n=(n) wweights=1
FastGaussTransform /WDTH=(bw)/RX=(4*bw) /OUT1={xmin,nx,xmax} w,wweights // you may need to tweak /RX flag value
wave M_FGT; kde_norm=sum(M_FGT)*deltax(M_FGT); M_FGT /= kde_norm
string wn=NameofWave(w)+"_kde"; duplicate /d/o M_FGT $wn
killwaves M_FGT
End

Forum

Support
Gallery
Igor Pro 9
Learn More
Igor XOP Toolkit
Learn More
Igor NIDAQ Tools MX
Learn More