
Bode (magnitude and phase response of a linear transfer function)

bech
Sun, 01/09/2011 - 09:26 am
Because Igor is sorely lacking in support for linear systems, the format of the transfer function is a bit free-form. One day, it would be nice for Igor to have a linear system structure that would automatically handle features such as continuous or discrete dynamics, different representations (Laplace domain, pole-zero, state space, etc.), and the like. For now, this will do.
Example:
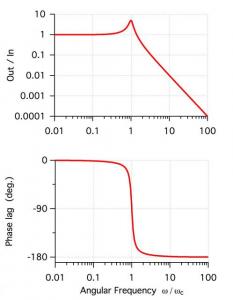
•Make /o/d/n=1 pw={0.1} // create a parameter wave; set the damping to zeta=0.1
•Bode(SecondOrder,pw,0.01,100,1000,"order2")
•Display order2_mag vs order2_omega // these are the minimal graphics commands
•ModifyGraph log=1 // the attached layout has been "prettied up" in inessential ways
•Display order2_ph vs order2_omega
•ModifyGraph log(bottom)=1
•Bode(SecondOrder,pw,0.01,100,1000,"order2")
•Display order2_mag vs order2_omega // these are the minimal graphics commands
•ModifyGraph log=1 // the attached layout has been "prettied up" in inessential ways
•Display order2_ph vs order2_omega
•ModifyGraph log(bottom)=1
Here are the Igor functions:
//_______________________________________________________________________
Function Bode(tf,pars,w0,w1,N,base) // make waves for Bode plots (mag & phase) for transfer function
FUNCREF myprotofunc tf // pass function as argument; tf = "transfer function"
Wave pars // parameter wave to pass to function
Variable w0,w1,N // w0 = lower, w1 = upper frequencies; N = num points
String base // base name for output waves
String OmegaString=base+"_omega", BodeMagString=base+"_mag", BodePhString=base+"_ph"
Make /o/d/n=(N)$OmegaString,$BodeMagString,$BodePhString
Wave OmegaWave=$OmegaString, BodeMagWave=$BodeMagString, BodePhWave=$BodePhString
OmegaWave = w0*(w1/w0)^(p/(N-1)) // even spacing on log
Variable /c i=cmplx(0,1) // define i=sqrt(-1)
Make /free/c/d/n=(N) ss = i*OmegaWave // temporary wave for s = iw
BodeMagWave = cabs(tf(pw,ss)) // magnitude of frequency response
BodePhWave = atan2(imag(tf(pw,ss)),real(tf(pw,ss)))*180/pi // output phase in degrees
Unwrap 360, BodePhWave // prevent any 360 degree phase jumps
End
Function/c myprotofunc(pars,s) // format of prototype function (transfer function)
Wave pars; Variable /c s // pars = parameters; s = Laplace domain
End
//_______________________________________________________________________
Function/c SecondOrder(pars,s) // substitute your own transfer function here
Wave pars; Variable/c s
Variable zeta=pars[0] // zeta = dimensionless damping coefficient
Return 1/(1+2*zeta*s+s^2) // standard scaled 2nd-order response function
End
//_________________________________________________
Function Bode(tf,pars,w0,w1,N,base) // make waves for Bode plots (mag & phase) for transfer function
FUNCREF myprotofunc tf // pass function as argument; tf = "transfer function"
Wave pars // parameter wave to pass to function
Variable w0,w1,N // w0 = lower, w1 = upper frequencies; N = num points
String base // base name for output waves
String OmegaString=base+"_omega", BodeMagString=base+"_mag", BodePhString=base+"_ph"
Make /o/d/n=(N)$OmegaString,$BodeMagString,$BodePhString
Wave OmegaWave=$OmegaString, BodeMagWave=$BodeMagString, BodePhWave=$BodePhString
OmegaWave = w0*(w1/w0)^(p/(N-1)) // even spacing on log
Variable /c i=cmplx(0,1) // define i=sqrt(-1)
Make /free/c/d/n=(N) ss = i*OmegaWave // temporary wave for s = iw
BodeMagWave = cabs(tf(pw,ss)) // magnitude of frequency response
BodePhWave = atan2(imag(tf(pw,ss)),real(tf(pw,ss)))*180/pi // output phase in degrees
Unwrap 360, BodePhWave // prevent any 360 degree phase jumps
End
Function/c myprotofunc(pars,s) // format of prototype function (transfer function)
Wave pars; Variable /c s // pars = parameters; s = Laplace domain
End
//_______________________________________________________________________
Function/c SecondOrder(pars,s) // substitute your own transfer function here
Wave pars; Variable/c s
Variable zeta=pars[0] // zeta = dimensionless damping coefficient
Return 1/(1+2*zeta*s+s^2) // standard scaled 2nd-order response function
End
//_________________________________________________

Forum

Support
Gallery
Igor Pro 9
Learn More
Igor XOP Toolkit
Learn More
Igor NIDAQ Tools MX
Learn More