Stochastic ODE: Euler-Maruyama illustrated
Stochastic ordinary differential equations have their own issues and require numerical methods that differ from those used for deterministic ODEs. While Igor does not support stochastic ODEs in an operation, it is straightforward to code explicitly the (simple) Euler-Maruyama (EM) method. In learning how to deal with such equations, I made the following code, which simulates a particle in a double-well potential of adjustable depth. It could be the starting point for explorations of stochastic resonance, information processing by small systems, etc. For this particular case, the EM method works well. For other applications, other algorithms such as Milstein's or Heun's methods may give better results. Note that the program uses 2 implicit loops, one to loop over the N time steps of an individual path, the other to calculate M paths.
If others are interested in stochastic methods, I encourage you to post more examples. This will perhaps persuade the Igor folks to add explicit support for stochastic equations. (While these methods are easy to program in Igor as it stands, they are much slower than what a C-coded version could do. And these calculations tend to require LOTS of iterations.....)
Note that this was developed in 6.10b07, but I see no reason that it won't run in Igor 6.0x.
//________________________________________________________________ function em(M,N,D,Tf) // vector implementation of Euler-Maruyama variable M,N,D,Tf // M = paths, N = time points // D = noise strength, Tf = final sim. time // try M=1, N=1e4, D=0.01, Tf=1000 // SetRandomSeed 0.5 // useful for debugging variable dt = Tf/N, Xzero = 0 // dt = time step; Xzero = initial condition wave pars // declare parameter wave make /o/n=(M,N) dW dW = sqrt(2*D*dt)*gnoise(1) // M realizations of noise terms dW(t) Integrate /meth=2 /dim=1 dW /D=W // integral is just sum of dW's Duplicate /o W, Xem Xem[][0] = Xzero // initialize all paths Xem[][1,N] = Xem[p][q-1] + dt*myfunc(pars, (q-1)*dt, Xem[p][q-1]) + dW[p][q-1] // this is the crucial step for the EM method! 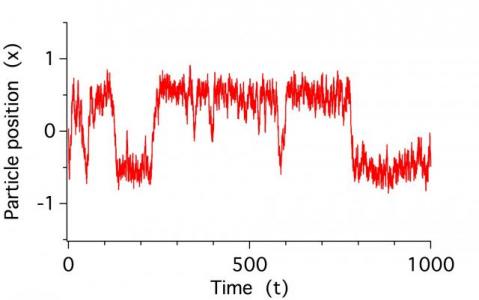MatrixOp /o Xem0 = row(Xem,0)^t // get a single trajectory to graph SetScale/P x 0,dt,"", Xem0 killwaves dW,W,Xem // get rid of big waves end //________________________________________________________________ Function myfunc(pw,t,x) wave pw; variable t,x // t for time-dependent forces; not needed here variable a=pw[0] // barrier height (try a=0.3) return a*x - x^3 // force = -dU/dx, U = -a*x^2/2 + x^4/4 End //________________________________________________________________ Window path_graphs() : Graph PauseUpdate; Silent 1 // building window... Display /W=(533,50,1004,389) Xem0 ModifyGraph width=360,height=216 ModifyGraph marker=19 ModifyGraph msize=1 ModifyGraph nticks(bottom)=2 ModifyGraph fSize=18 ModifyGraph manTick(left)={0,1,0,0},manMinor(left)={1,0} ModifyGraph manTick(bottom)={0,500,0,0},manMinor(bottom)={4,0} Label left "Particle position (x)" Label bottom "Time (t)" SetAxis left -1.5,1.5 ControlBar 42 SetVariable setvar0,pos={67,8},size={214,27},title="barrier height a ",fSize=18 SetVariable setvar0,limits={0,1,0.1},value= pars[0] EndMacro